In questa sede spiegheremo come utilizzare alcune semplici procedure statistiche al fine di ottenere maggiori informazioni dai punteggi ricavati dalle prove oggettive. Utilizzeremo un linguaggio molto semplice in quanto l’esperienza ci insegna che nei confronti della statistica esiste una sorta di avversione dettata, probabilmente, da pregiudizi nei confronti di “ciò che è matematico in generale”.
Per il necessario approfondimento suggeriamo il seguente volume:
M. Notti, Modelli statistici per la ricerca educativa, PensaMultimedia, Lecce-Brescia 2003.

1. La media aritmetica

La media aritmetica (come è noto) si ottiene sommando i singoli punteggi e dividendo poi il risultato per il numero dei punteggi stessi.

ESEMPIO
nel caso seguente:

punteggi ottenuti dagli allievi: 7 8 12 15 16 18 21 22

per conoscere la media è necessario sommare i punteggi:

(7 + 8 + 12 + 15 … ) = 119

e dividere poi il risultato per 8;

La media = 119/8 = 14,875

In ambito didattico: Tanto più la media dei punteggi sarà elevata (e quindi più vicina al punteggio massimo), tanto più gli allievi avranno dimostrato di essere padroni delle abilità culturali perseguite.

2. La mediana

Per calcolarla è necessario innanzitutto predisporre i risultati in ordine crescente o decrescente; la mediana si pone al centro della serie di punteggi, sicché avrà al di sopra di essa un numero di risultati uguale a quello che sta al di sotto.

ESEMPIO
Supponiamo di avere i seguenti punteggi:

1 2 2 6 7 9 12

In questo caso il valore della mediana è 6. Si può vedere che sul lato destro della mediana sono presenti 3 punteggi (7, 9, 12), come su quello sinistro (1, 2, 2). Nel caso in cui il numero dei punteggi fosse pari, per calcolare la mediana sarebbe necessario conoscere la media aritmetica dei 2 punteggi che stanno al centro.

L’utilità della mediana risiede, principalmente, nel confronto che è possibile istituire con la media; confronto che conduce a una delle tre situazioni seguenti.

 A. 1,1,2,3,4,4,5,8,8,11,15,20,25

La mediana è 5;

la media è 8,23.

In ambito didattico: La mediana è inferiore alla media; ciò vuol dire che più della metà dei discenti ha ottenuto punteggi infe­riori alla media. Non è una situazione auspicabile dal punto di vista didattico.

B. 1, 1, 1, 1,4,5, 6, 6, 6, 7, 8, 8, 9

La mediana è 6;

la media è 4,84.

In ambito didattico: In questo caso la mediana è superiore alla media; ciò vuol dire che più della metà dei discenti ha ottenuto punteggi superiori alla media. Una situazione auspi­cabile dal punto di vista didattico.

C. 2, 3, 5, 7, 8

La mediana è 5;

la media è 5.

In ambito didattico: In questo ultimo caso media e mediana coincidono. Perciò metà degli allievi ha ottenuto risultati inferiori alla media e l’altra metà superiori. Metà della classe è ancora al di sotto delle prestazioni medie; è certo un risultato mediocre.

3. La deviazione standard σ

Per comprendere l’andamento di una serie di risultati con sempre maggiore precisione, è necessario fare rife­rimento a operazioni più complesse: ci soffermeremo sullo scarto quadratico medio (o deviazione standard). Attraverso di esso siamo in grado di capire quanto i sin­goli risultati si distanziano, mediamente, dalla media, e quindi di conoscere il loro grado di dispersione. Nel caso delle prove oggettive, ad esempio, con il calcolo della deviazione standard veniamo a conoscenza del­l’intervallo che separa, in media, ogni singolo punteggio dalla media. Ne consegue che:
– il valore della deviazione standard aumenta (rispetto al valore della media) quanto più i pun­teggi della serie sono distanti dalla media;
– il valore della deviazione standard diminuisce (rispetto alla media) quanto più i punteggi della serie sono vicini alla media.

Questa la sua formula:

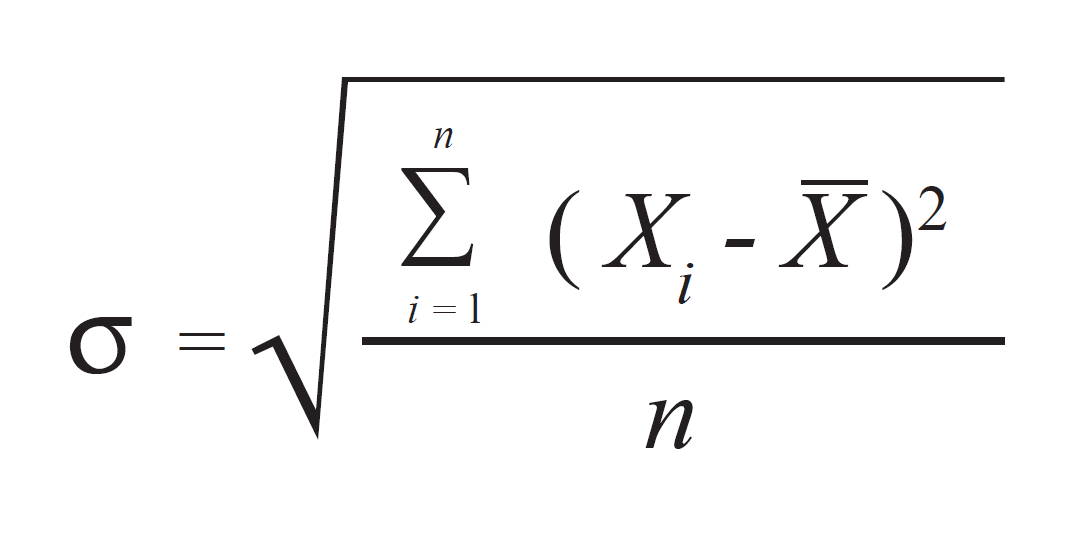dove:
x_i = valore dell’i-esimo punteggio
 = media aritmetica dei punteggi
n = numero dei punteggi della serie

In ambito didattico: se il valore della deviazio­ne standard non supera il 10-12% rispetto a quello della media, ciò vuol dire che i risultati ottenuti dalle prove strutturate sono abbastanza uniformi. Se invece il valore della deviazione standard va oltre, sarà bene suonare un campanello di allarme; si dovrà cercare di capire, cioè, perché i discenti hanno conseguito risultati così diversificati e, di conseguenza, impostare diversamente l’itinerario didattico.

ESEMPIO
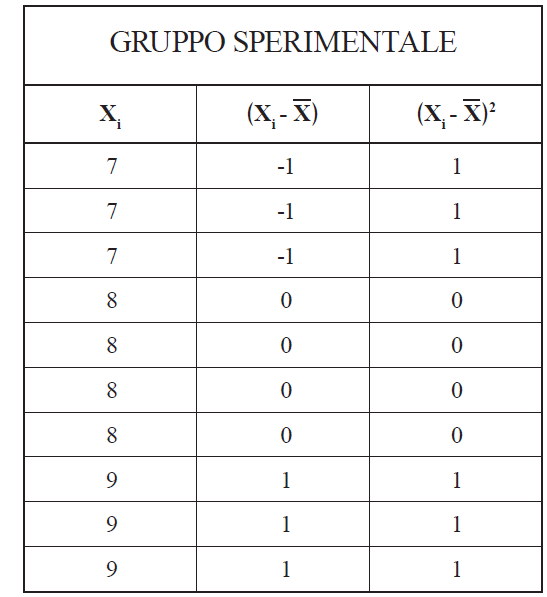
Al termine di una sperimentazione didattica si voglio­no confrontare i punteggi ottenuti dal gruppo speri­mentale rispetto a quelli del gruppo di controllo. Dalla elaborazione dei punteggi della prova oggettiva, som­ministrata a entrambi i gruppi, abbiamo ottenuto le seguenti serie di punteggi:
G S: Media(7,7, 7,8,8,8,8,9,9,9) = 80 / l0 = 8
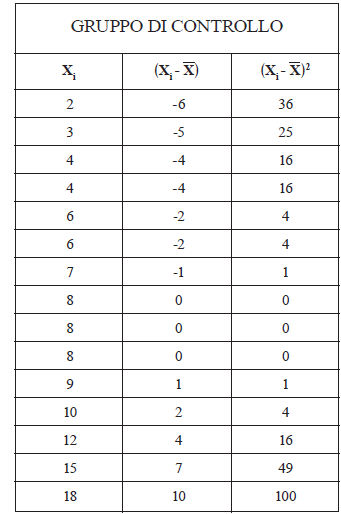
G C: Media(2, 3, 4, 4, 6, 6, 7, 8, 8, 8, 9, l0, 12, 15,18) = = 120/15 = 8

Vediamo i passaggi in successione:
– nella 1 prima colonna a sinistra si inseriscono i pun­teggi;
– nella seconda colonna si inseriscono gli scarti di ogni singolo punteggio rispetto alla media;
– nella terza colonna si inseriscono i quadrati degli scarti riportati nella seconda colonna.
Così, sommando i valori della terza colonna, ottenia­mo il valore 6; applicando poi la formula, si ottiene: 0,77.
In questo caso il valore della deviazione standard si aggira intorno al 10% del valore della media. Pertanto, siamo in presenza di una sostanziale omogeneità delle prestazioni degli allievi.

Evitiamo ora di riportare tutti i passaggi; sommando i valori della terza colonna otteniamo 272; applicando poi la formula, si ottiene 4,25.
Contrariamente a quanto visto sopra, in questo caso il valore della deviazione standard è ben al di sopra del 10-12% della media, e anzi supera addirittura il 50% del valore medio. Siamo quindi in presenza di una marcata disomogeneità delle prestazioni.
Nei due casi appena visti, la media è la stessa, ma la distribuzione delle competenze nelle due classi è molto diversa. Infatti nel primo caso i punteggi sono quasi tutti vicini alla media mentre nel secondo è evi­dente una variabilità molto più pronunciata.